til

コンピュータアーキテクチャ, OS, 電子回路, 論理回路 (computer architecture, operating system, electronic circuit, logical circuit)

ページ構成の際、次の情報源を参考にした。

数体系・符号体系

n進数の小数部

n進数の小数部

基数変換 (radix conversion)

n進数→10進数は次のように考える。4,000（よんせん）は40 00（よんじゅう ひゃく）と考えることができる。同様に、0.05 = 5厘（ごりん）は0.5分（れいてんごぶ）とも考えられる。このように、指数の絶対値が大きい桁の数字による数は、指数の絶対値が小さい桁の数字でも表せる。n進数→10進数の変換では、$n^{ m }$の倍数を$n^{ m -1}$の倍数で表す操作を繰り返す。

また、10進数→n進数は次のように考える。指数の絶対値が小さい桁の数は、指数の絶対値が大きい桁の数としては表すことができない。（ここで4は0.4 10と言い出すとややこしいので一旦考えない）そのため、nで割って/掛けて、余り/整数部を指数の絶対値が小さい桁の数にする。

最後に、n進数・10進数間の変換について表と図にまとめた。

変換\部分 整数部 小数部
n進数→10進数 大きい桁から順に、nを掛けて1つ小さい桁の値と足す、を繰り返す 小さい桁から順に、nで割って1つ大きい桁の値と足す、を繰り返す
10進数→n進数 nで割って余りを取り出し、下位桁に並べるのを繰り返す nを掛けて整数部を取り出し、上位桁に並べるのを繰り返す

n進数

補数 (complement)

足すと基数になるものが補数である。例えば、876の10の補数(1000の補数とは言わない)は124である。

要するに1000からその数を引けば求められるのだが、代わりに999から引いて1を足して求めると繰り下がりがなくて計算しやすい。各桁の9の補数を求めて、その値を連結して1を足すとも言える。

同様に、16の補数、2の補数などn進数の補数が存在する。2の補数を求めるためには、各桁の1の補数を求めて、その結果を連結して1を足すことになる。つまり全桁を反転させてから1を足すのに等しい。この全桁を反転させた値も1の補数と呼ぶが、それ以外の補数の定義とは違って紛らわしいのでやめたほうがいいと思う。

論理演算

MIL記法

米軍の物資調達のために開発された米軍ミル企画の一つである、MIL-STD-806に基づいた論理回路の記法。

組み合わせ回路 (combinational logical circuit)

入力値の組み合わせのみによって出力が決まる回路を組み合わせ回路という。加減算器、エンコーダ・デコーダ、マルチプレクサなどを含む。組み合わせ回路は状態を保つことができない。

いきなり回路設計に入ると却って時間がかかるので、次の手順を踏むこと。

  1. 真理値表による定式化
  2. 簡単化
    1. 加法標準形から論理式を整理する
    2. カルノー図 (Karnaugh map)によって隣接する項をまとめる
    3. クワイン・マクラスキー法 (Quine-McCluskey method)によって隣接する項をまとめる
  3. 回路記述

加法標準形・乗法標準形は、各項が真理値表の1行に対応する（つまり全ての論理変数が含まれる）論理関数である。出力が1になる行のORとして表されるのが加法標準形である。出力が0になる行の否定のANDとして表される（つまり、どの0にも該当しない）のが乗法標準形である。

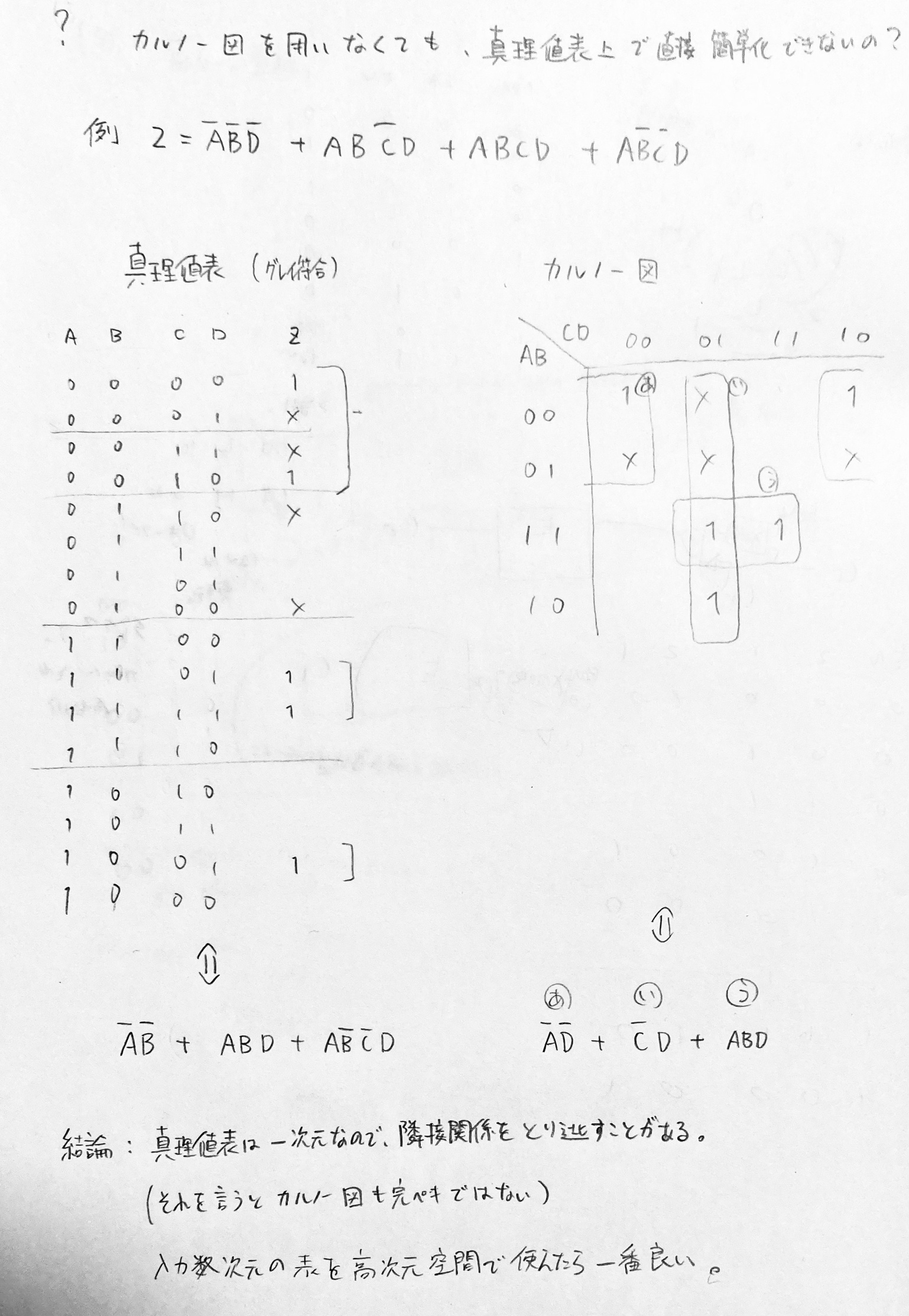
カルノー図は、2次元の表の軸にグレイ符号を用いて入力を記し、それぞれのマスに出力を記載した表である。

[!NOTE] 真理値表をグレイ符号で書いたらカルノー図の代わりになる？ 入力数が少ないならそれでもいいかも。理想的には入力数次元の高次元トーラスで論理的隣接性を見るのが良さそう。紙面上で4次元以上を扱うなら素直にカルノー図が良い。

真理値表とカルノー図の比較

加減算器

キャリールックアヘッド

m桁のn進数は$m^n$までの数値を表すことができる。$m^n$より大きい数値を表すには、新たな桁を用いる。したがって、数値が$m^n$を超える場合には桁上りが生じる。論理回路は数値を2進数で表すため、$桁数^2$を超えると桁上りが生じる。具体的には、2進数におけるn桁目の繰り上がりの判断は、n桁目がともに1（$A_n \cdot B_n$）であるか、またはN桁目のいずれかが1かつn-1桁目が繰り上がり（$(A_n \oplus B_n) \cdot C_{n-1}$）で行われる。

2024年現在に一般的な64ビットのCPUは、64桁の2進数の加算ができる。桁上りを考慮すると各桁の加算処理を並列化できないため、大きな桁になるほど計算に取り掛かるのが遅くなる。ところで、桁上りには大まかに次の2通りがある。

  1. 生成(generate)
  2. 伝播(propagate)

$i+1$桁目のキャリーインを$c_{i+1}$と表すとき、入力について$a_i \cdot b_i$の場合を生成という。それに対して、$p_i = a_i + b_i$として、$p_i \cdot c_i$を伝播という。伝播は再帰的に使えるから、桁上げは次のように表せる。

$c_{i+1} = g_i + (p_i \cdot g_{i-1}) + (p_i \cdot p_{i-1} \cdot g_{i-2}) + (p_i \cdot p_{i-1} \cdot … \cdot g_0)$

このように、ある桁で桁上りの判断に必要なOR演算を行うことを、前桁の出力を待つ方式と比べてキャリールックアヘッド(桁上げ先見, carry-lookahead)加算器という。桁数をmとすると、m桁分の伝搬のAND演算がボトルネックであり、計算量は$log_2N$となる。とはいえ、この方式を64ビットまで続けると必用な論理回路の数が膨大になってしまう。キャリールックアヘッドを備えた4ビット程度の加算器を作り、それを順次桁上げ方式で連結することで、バランスの良い論理回路になる。

個人的な意見だが、キャリールックアヘッド処理の本質を捉えるには、「前桁の出力を用いず、入力を直接用いる」という説明は不正確である。更に、「繰り上がりがあり得る全てのパターンを並列に処理し、最後にORを取る」という説明も不十分と考える。例えば、$A=00001$と$B=01111$の足し算では、$A \cdot B = 1$かつ$A_n \oplus B_n = 1 n = 2,3,4,5$のパターンで繰り上がりが起きるが、まず1桁目を加算、次に2桁目と2桁目のXORのAND…と順番に処理していたら、前桁の出力を用いるのと計算量が変わらない。そうではなく、n入力のANDゲートを用いることで、$((A_1 \cdot B_1) \cdot (A_2 \oplus B_2)) \cdot((A_3 \oplus B_3)\cdot(A_4 \oplus B_4))$のように各桁のANDを取るのが並列化され、最も時間のかかるパターンの計算量を$log_2N$に抑えられるのである。

エンコーダ・デコーダ

マルチプレクサ・デマルチプレクサ

順序回路

クロック

自らの出力を入力に使うことで値を保持するような、簡単な順序回路を作りたい。例えば、外部からの入力が0であれば内部の値を出力し、1であれば値を反転させるT回路を考える（ちなみにこれはT型フリップフロップである）。T回路がある瞬間に外部から1を受け取ると、出力Qは反転する。回路の設計者の意図としては、ちょうど出力Qが反転したところで、外部からの入力を0にしたい。しかし電流は物理的な現象だから、そのようにピッタリ動作させることは難しい。結果として、外部からの入力が1である間、T回路の出力Qが発振、つまり0と1を高速で切り替え続けるだろう。

これに対して、順序回路の更新のタイミングを指定する仕組みを考える。結論から言えば、論理回路の状態と無縁な時計（クロック）によって決まる時間（サイクル時間）に従って1と0を切り替える入力を設け、すべての回路はそのタイミング（クロック周期）でのみ状態を切り替えることにすると良い。このような回路を同期回路という。

サイクル時間は1秒未満の僅かな時間なので、処理速度について話す時はその逆数であるクロック周波数を用いると良い。2024年現在販売されているCPUであれば、クロック周波数は2.4GHz等である。これは、CPUのアーキテクチャによって異なるものの、大まかに言えば1秒間に$2.4 \times 10^9$の演算ができる。サイクル時間が短いほど多くの演算ができるが、回路内の信号が安定するまでは待つ必要があり、それがサイクル時間の下限となる。

クロックを持たない回路を非同期回路という。クロック信号配線が短くなる、クロック周期を待たずに演算ができるために速いといった利点があるが、設計が難しい等の理由から普及していない。[^dwm_2005] [^dwm_2005]: 非同期回路設計のすすめ

CPUのクロック周波数をメーカーが保証する値よりも引き上げることをオーバークロックという。動作が不安定になるが、処理速度の向上が期待される。近年はマザーボードが複数のシステムクロックの生成に対応しており、ハードウェアの改造なく試すことができる。

フリップフロップ (flip-flop)

入力とクロック入力を備え、クロックが1である（アサートされた）間は入力に応じて状態を変えるが、クロックが0である（ネゲートされた）間は状態を出力する回路をラッチ(latch)という。ラッチの問題点は、クロックがアサートされている間出力が発振してしまうことである。そこで、クロックのエッジ、つまり立ち上がりと立ち下がりでのみ値が更新されるような回路をフリップフロップという。ラッチとフリップフロップを総称して、広義のフリップフロップということもある。値を入力すると状態が変わるように見えるため、フリップフロップという名前といわれている。[^renesas_flipflop] [^renesas_flipflop]: 順序回路、フリップフロップ

フリップフロップの種類について、次の通りまとめる。

[!NOTE] なぜSRラッチにSet/Resetが必要なのかを自分なりに考えたが、入力が1つでは保持した値の取り出し・0のセット・1のセット、という3種類のコマンドを表現できないためという結論になった。High/Lowに加えてNullがある世界なら入力が1つのSRラッチが存在するかもしれない。
また、現実世界でフリップフロップに相当するものがないかを考えた。電流のように流れ続けるが、初期の入力を保ち続けるものがないだろうか。水泳のインターバルトレーニング（サイクル）が相当するなと思った。25mを40秒サイクルで回るとき、1~40, 81~120, …秒目にいる方が、スタートしたプールサイドである。

フリップフロップの分類を、次の通り表にした。

入力 ラッチ フリップフロップ マスタスレーブ エッジトリガ
SR ◯ ◯ ◯ ◯
D ◯ ◯ ◯ ◯
JK - - ◯ ◯
T - - ◯ ◯

レジスタ

[!NOTE] プログラミング中に明示的にレジスタを読み書きしたことないですけど？というのが気になった。
例えばHackプラットフォーム2では、CPUに対するメモリ入力が1つだけのため、2つのメモリの値を対象に操作する（比較・四則演算・代入など）場合、片方をCPU内のデータレジスタに保存する必要がある。
制約がそれだけなら、メモリ入力を2つにすることで解決できそうだ。しかし、高級言語での1命令が機械語で複数命令になり、かつ1つの値を連続して使う場合はどうだろうか。
例えば数の3乗はどうか。おそらく機械語では、乗算を2回行うと思われる。その場合、毎回メモリの値を要求していては時間がかかる。そのような場合に備え、内部的にレジスタに値を保持するようにコンパイルしていると考えれば良さそうだ。

電子回路

電子回路の中でも半導体を用いて微細な回路を作ったものを集積回路 (IC, integrated circuit)といい、中でも支配的な技術がCMOS (Complementary Metal Oxide Semiconductor, 相補型金属酸化膜半導体)である。

CMOSはプロセッサだけでなく、無線通信のための回路にも用いられており、これをCMOS RF技術と呼ぶ。[^xtech_CMOS_RF] [^xtech_CMOS_RF]: 第1回：ワイヤレス通信とRF回路の歴史からCMOS RF回路への道を見る

集積回路の古典的な技術としてTTL (Transistor Transistor Logic)がある。

ハードウェア記述言語 (HDL, hardware description language)

論理回路を設計するためのDSL。論理回路をRTL (レジスタ転送レベル, register transfer level)、つまりCPUやレジスタなどのブロック図のレベルで記述する。VHDLやVerilogなどの種類がある。電子回路と1対1対応するゲート回路の生成にあたっては、論理合成 (logic synthesis)というプロセスを経る。これはブロック図をゲート回路に変換した上で、クワイン・マクラスキー法に代表される論理最小化を行って回路を最適化する。

また、C言語などで記述されたプログラムをハードウェアのロジックに変換する手法を高位合成 (HLS, high level synthesis)と言う。有名な高位合成のシステムとしてはVivado HLSがある。

ECL (エミッタ結合論理, Emitter-coupled logic)

TTLやCMOSに比べて高速な論理回路の実装方式。消費電力と発熱量が多い欠点がある。

FPGA

ロボット制御など、画像処理において速度が極めて重要、かつ電力が限られている場合、GPUに代わって専用チップでの処理が考えられる。しかし、カスタム・セミカスタムのチップはコストが高く、制約も多い。これに対して、開発者が手元で配線できるデバイスをFPD (Field Programmable Device)といい、中でも組み合わせ回路だけのものをPLD (Programmable Logic Device)、フリップフロップを持つものをFPGA (Field Programmable Gate Array)という。FPGAの種類は多く、$150ほどでRaspberry Pi程度の大きさの基盤（Artix 7など）から、$10,000ほどで30cm四方程度の大きさの基盤（AMD Virtex UltraScale+など）まである。

機械語 (machine language)

コンピュータに物理的操作を行わせるための、0と1からなる語を機械語という。+のような演算子 (operator)と演算対象 (オペランド, operand)からなる。

機械語とだいたい1対1で対応する、人間が理解するための言語がアセンブリ言語 (assembly language)である。

命令セット (instruction set)

機械語の集合を命令セットという。CPUのアーキテクチャによって実行可能な命令セットが異なる。例えばx86系命令セット, ARM系命令セット, MIPS系命令セット, RISC-V系命令セット等がある。命令セット及びCPUやレジスタ等の実行環境をまとめて命令セットアーキテクチャ (ISA, instruction set architecture)という。

ISAの設計の方向性には、CISC (シスク)とRISC (リスク)がある。CISCが単一の命令で複数の処理を行うなど複雑である一方で、RISCは命令の総数や種類を減らす思想であった。これは、初期のプログラミング環境ではコンパイラが存在せず、機械語やアセンブリ言語で直接プログラミングを行っていたためである。[^wikipedia_RISC] [^wikipedia_RISC]: RISC

2010年頃から設計が始まった比較的新しいISAがRISC-V (リスクファイブ)である。チップベンダーの保有するISAに沿ったCPUを開発するためにはライセンス費用を払う必要があるが、RISC-Vはオープン規格のためその必要がない。

[!NOTE] RISC-Vの開発にあたって、CやPythonなどプログラミング言語のコンパイラは誰が対応したの？

バイナリ変換

特定のプラットフォームの機械語にコンパイルされたプログラムを、異なるプラットフォームで動かすことを考える。実行ファイルの一部は実行時にしかジャンプしないため、動的に機械語を読み替える必要がある。そのような機械語の変換技術をバイナリ変換という。

AppleがApple Silicon発売時にx86向けアプリケーションをサポートした技術はバイナリ変換である。具体的には、Rosetta2を用いてバイナリを変換した。[^sergio_2020] [^sergio_2020]: Rosetta 2のx86からarm64への変換はどのように動作するのか

コンピュータにおける算術演算

プロセッサ

CPU

CPUは、ノイマン型コンピュータにおける演算装置と制御装置を担う。CPUの構成要素は次の通り。

パイプライン処理

自動車の製造のような、複数の工程がある作業を考える。処理のスループットを引き上げるとする。1人で全ての組み立てを行う職人の数を増やすのではなく、工程を分けて流れ作業とし、同時に複数台を製造する手法を、パイプライン処理という。コンピュータの処理については、次の工程に分けられる。

  1. 命令フェッチ
  2. 命令デコード
  3. 演算
  4. 結果の格納

[!NOTE] CPUがメモリをフェッチする、という表現が不思議だったのだが、毎クロックメモリ自体は読んでいて、次のクロックで読みたいアドレスを出力しておく、という言い方ならしっくり来るかも。

1クロック毎に1工程を処理する。異なる命令の各工程を同時に処理しているため、処理が終わった後すぐに次の工程にデータを送ると混乱が生まれる。そこで、各工程の間にレジスタを挟み、これをパイプラインレジスタという。

パイプラインハザード

命令をクロックごとに動作させられない状態をパイプラインハザードという。パイプラインハザードは、原因によって3つに分類できる。ハザードによって命令の実行が止められる状態をストール(stall)という。

種類 原因 対策
構造ハザード（Structural Hazard） 複数の命令が同時に同じハードウェアリソース（メモリやレジスタなど）にアクセスしようとする状況。 資源の多重化
データハザード（Data Hazard） ある命令が、まだパイプライン内にある前の命令の結果に依存している状況。 フォワーディング（計算結果を次の命令に直接転送）、パイプラインのストール、コンパイラによる命令のスケジューリング。
制御ハザード（Control Hazard） 分岐命令によってプログラムの実行フローが変更される可能性がある状況。 分岐予測、投機実行、遅延分岐（分岐命令の直後に、分岐に関係なく実行される命令を配置）。

構造ハザードにおける資源とは、例えばメモリバスを指す。パイプラインの異なる工程でそれぞれ命令フェッチとデータアクセスが行われる場合、命令とデータでキャッシュが同一だと、競合が起きることがあった。

命令レベル並列処理とアウトオブオーダ処理

1プロセッサ内に複数のALUを配置し、命令デコードの工程で命令の依存関係も考慮しつつ、逐次系のプログラムを並列実行可能にするあアーキテクチャをスーパースカラという。それに対して、並列実行すべき命令の組をコンパイラが予め指定する方式に対応したプロセッサをVLIW (very large instruction word)という。[^onur_2023]VLIWは機械語の工夫で性能を引き上げる反面、プロセッサを改良すると機械語の互換性がなくなるためプログラムを新たにコンパイルする必要があり、下火になった。[^xtech_VLIW] [^onur_2023]: 特別な読みがあるのかと思ったら、普通に「ヴィエルアイダブリュー」だった。VLIW Architectures | Onur Mutlu Lecturesを参照した。 [^xtech_VLIW]: VLIW

ハザードを減らして命令の並列度を上げるために、コンパイラが機械語プログラムを最適化することを静的最適化 (static optimization)という。それに対して、命令をスケジューリングする際に順序を入れ替えることをアウトオブオーダ (out of order)処理といい、逆に入れ替えをしないことをインオーダー (in order)処理という。アウトオブオーダ処理の中でも、命令を演算実行ステージに入れる順番の入れ替えをアウトオブオーダ実行、実行結果をレジスタに格納する順番の入れ替えをアウトオブオーダ完了という。

アウトオブオーダ処理による並列実行を考えると、考慮すべきデータハザードの種類が増える。命令Aの結果を命令Bで参照することをフロー依存といい、これによって引き起こされるデータハザードをRAW(Read After Write)ハザードという。フロー依存を防ぐことはできない。一方で、処理を並列化したことによって、異なる命令がたまたま同じレジスタを使うことがある。命令Aで読み出したレジスタに命令Bが書き込みを行う依存関係を逆依存といい、これによって起きるハザードをWARハザードという。また、命令Aで書き込んだレジスタに命令Bが再度書き込みを行う依存関係を出力依存といい、WAWハザードの要因となる。

逆依存と出力依存はレジスタ数が十分にあれば解決できる。しかしレジスタ数には限りがあるから、レジスタ番号を置き換えることで解決する。これをレジスタリネーミングという。ハードウェアで動的にレジスタ番号を置き換える方法にマッピングテーブルが、連想機構をもつ目盛によってレジスタリネーミングを実現する方法にリオーダバッファがある。

入出力装置

入出力装置はCPUに対して抽象化されているべきであり、その方法がメモリマップドI/Oである。すべてのデバイスは、CPUから見るとメモリ上の領域に過ぎない。

記憶階層

メモリ (memory)

記憶装置。ランダムアクセス構造のメモリでは、固定幅のセルが連続して並んでおり、この固定幅のセルを「ワード」「ロケーション」と呼ぶ。

メモリの特性を測るための数値がいくつか存在する。

メモリの構成要素は次の通り。

メモリの種類は次の通り。主記憶装置・補助記憶装置のいずれの役割も考えられる。

[!NOTE] 読み書き可能であることは、メモリが主記憶装置である必要条件ではない。言い換えると、読み込み専用の主記憶装置も普通にありえる。 組み込みシステムやBIOS、UEFIファームウェアはROMが主記憶装置の役割を果たしているとみなすことができる。

キャッシュと仮想記憶

CPUとレジスタを用いた演算にかかる時間に対して、メモリからデータを読み取ることは時間がかかるため、キャッシュが活用されている。同様に、HDDやSSDなどのストレージへのアクセスを避けるため、メモリとストレージを透過的に扱うための抽象化された記憶装置を設ける戦略があり、その記憶装置を仮想記憶と呼ぶ。仮想記憶の用途は大別すると次の2つである。

  1. 仮想マシンにメモリを割り当てる。歴史的には、タイムシェアリング・システムにおいて多くのプログラムでコンピュータを共有する動機があった。
  2. CPUにメモリとストレージとを透過的に扱わせることで、メモリ上でのキャッシュを可能にする。

Webアプリケーション開発においては、キャッシュと言えばCloudFrontのようなCDNを指す。コンピュータアーキテクチャにおいては、単にキャッシュといえばメモリをキャッシュすることを指す。HDDやSSDをメモリでキャッシュすることは仮想記憶と呼び区別される。仮想記憶においてキャッシュをミスすることはページ・フォールト (page fault)と呼ばれる。

[!NOTE] 必要なデータがストレージにしかないときにページフォールトになることは分かったけど、そもそもファイルシステムを経由せずストレージにアクセスするのっていつ？ プログラミングしていてストレージのデータを読み込むタイミングとして真っ先に思いつくのはファイルやフォルダにアクセスするときだが、それらの場合はデータがメモリ上にあることは期待されていない。 仮想記憶経由でアクセスされるストレージ上のデータとは、それがファイルシステムから読み込んだかどうかに関わらず、メモリに載り切らなかったデータである。メモリが逼迫しており、かつそれらのデータへのアクセス頻度が低い場合は、OSの判断でメモリからスワップ領域にデータが移される。これをスワッピング（swapping）という。また、ページ単位でのメモリ管理により、特定のページがメモリからストレージ（スワップ領域）に移されることをページング（paging）という。

仮想記憶は仮想アドレスをメモリとストレージの物理アドレスに読み替える。この表をページテーブルという。ページテーブルのキャッシュをTLB (Translation-Lookaside buffer)という。

データ更新方式 (replacement policy)

キャッシュに値を反映させるにあたって、その内容を都度メモリに反映するライトスルー方式 (write through algorithm)と、後でメモリに反映するライトバック方式 (write back algorithm)がある。次の表にまとめた。

観点 ライトスルー方式 ライトバック方式
実装 単純 複雑
キャッシュに対象のデータ語がないとき 直接メモリに書き込む 一旦キャッシュにコピーしてから書き込む
ライト命令の実行速度 ライトバッファの速度 キャッシュの速度
キャッシュライン書戻し 不要 キャッシュライン追出しのとき

ライトスルー方式で都度メモリにアクセスしていては実行効率が落ちてしまうので、通常はライトバッファと呼ばれる高速なメモリを設ける。キャッシュライン書戻しとは、データ語がキャッシュから追い出されるときのキャッシュからメモリへの同期をいう。

ブロック配置

メモリ上のデータをキャッシュから高速に読み出すには、どのように格納すればよいだろうか。唐突だが、和食の献立と配膳を考える。春の献立では筍ご飯に菜の花のおひたし、ふきのとうのお味噌汁。夏の献立では素麺にひじきの煮物、もずくスープ。[^king-penta_i-6]季節や日によって献立は異なるが、配膳はどうだろうか。副菜は左奥、主食は左手前、汁物は右手前である。[^maff_26_jireishuu-23] [^king-penta_i-6]: 和食献立の基本から季節別アイデアまで網羅！ [^maff_26_jireishuu-23]: ご存じですか？“和の配膳”

和食の配膳では、お椀への素早いアクセスを担保するため、献立のそれぞれの品目で役割が異なることに注目して並べ方を決めている。ここでメモリとキャッシュを考える。ユーザーが扱っているファイルは複数のメモリアドレスに跨ることが普通だから、キャッシュに同じ時期に載るデータはメモリアドレスが近所の可能性が高い。これを空間局所性という。メモリアドレスが近所ということは、アドレスの下位ビットは異なるということである。そこで、アドレスの下位ビット（例えば32ビットメモリアドレスで4ビット目から14ビット目）を数値と見做し（インデックス）、キャッシュラインのその番目に当たるデータを読み出せば、定数時間でアクセスできる。

観点 ダイレクト・マップ セット・アソシアティブ フル・アソシアティブ
セットの数      
セットあたりのブロック数      
該当ブロックを見つける方法      
キャッシュミス発生時      

キャッシュミス (cache miss)

キャッシュ・コヒーレンス (cache coherency)

マルチコア・マイクロプロセッサは、コアごとにキャッシュを持つ。例えば、Intel Core i7は、コア内にL1,L2キャッシュを、コア共有でL3キャッシュを持つ。あるコアがメモリ上の値を書き換えた際、その値を他のコアのキャッシュが参照していたら、情報の先祖返りに繋がってしまう。まして、L1,L2キャッシュは数十キロバイト〜数メガバイトの容量を持つから、十分現実的な問題である。

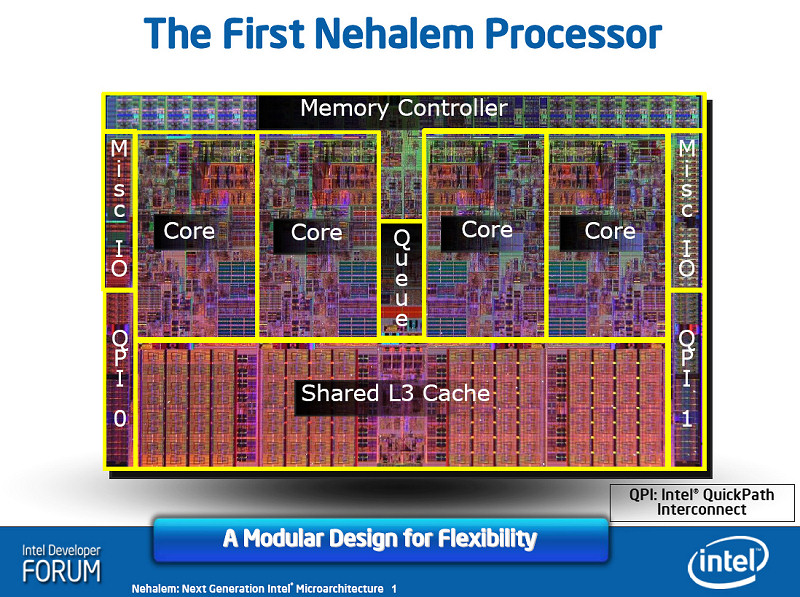
Core i7の内部構造

コア間でキャッシュの一貫性を保つことをキャッシュ・コヒーレンスという。方法としては、行が変更された際、変更したコア以外のコアにあるキャッシュを無効化することが考えられる。キャッシュに変更が起きる度にバスを通じてメッセージをブロードキャストする方式をスヌープ方式 (snooping)、スヌープキャッシュまたはバススヌーピングという。[^ibm_aix_cache-coherency]バスの状態を常に詮索(snoop)しているということ。 [^ibm_aix_cache-coherency]: キャッシュの整合性

並列プロセッサ

コンピュータの処理能力を上げるための手段としては、クロック周波数の引き上げやCPI(命令あたりクロック数, clock cycles per instruction)の改善等が挙げられる。しかし、マイクロプロセッサの冷却能力に限界があることから、クロック周波数を引き上げるような消費電力を増やす手段も同じく限界を迎えている。したがって、プロセッサの性能向上ではハードウェアの並列性の引き上げが行われるであろう。そのようなプロセッサをマルチコア・マイクロプロセッサ、通常は単に省略してマルチコアプロセッサと呼ぶ。マルチコアプロセッサは通常、共有記憶型マルチコアプロセッサ(SMP, Shared Memory Processor)である。

コンピュータの話では、並行(concurrent)と並列(parallel)の違いが重要である。複数の処理を切り替えながら進めるのが平行であり、複数の処理を同時に進めるのが並列である。

フリンの分類 (Flynn’s taxonomy)

並列処理は、処理あたりの命令の数とデータの数で次の通り分類できる。

命令流＼データ流 単一 複数
単一 SISD SIMD
複数 MISD MIMD

ハードウェア・マルチスレッディング

GPU

CPUが汎用的な計算を素早く行うのに対して、GPUは並列計算を得意としている。例えばIntel Core i9は24コアを搭載し、各コアが複数のALUを持つ。それに対して、NVIDIA RTX4090は16,384個のCUDA Coreを持つ。

現代のPCのような、CPUとGPUの混合によるシステムを異種混載システム(heterogeneous system)とも言う。また、非グラフィックスタスクをGPUに加えてGPUを用いて処理することをGPUアクセラレーションと言う。CUDAを例にすると、ホスト(CPU)からデバイス(GPU)にデータをコピーし、関数を実行し、計算結果をデバイスからホストにコピー、という流れを取る。

GPUプログラミング

CPUの世界では命令セットアーキテクチャに沿ったプロセッサの開発が行われているのに対して、GPUのハードウェアでは会社・世代を超えた機械命令の互換性がない。したがって、NVIDIAはPTX (Parallel Thread Execution)という命令セットを公開し、そのレイヤーで互換性を保証している。GPUを用いて汎用的な数値演算を行うにあたっては、従来はグラフィックスAPIとグラフィックスパイプラインを用いており、そうした汎用的な演算処理をGPGPU (general purpose computing on GPU)と読んでいた。それに代わって、並列プログラミング用の言語とAPIを用いて行うことはGPUコンピューティングと呼ばれる。

CUDA

NVIDIAのGPUプログラミング環境。

OpenCL

NVIDIAやAMDなどGPUを問わずに使えるGPUプログラミング環境。

Metal

macOSやiOSなどでサポートされるCG, GPGPUプログラミングのためのAPI。MSL (Metal Shading Language)を用いてプログラミングを行う。

マルチスレッド・マルチプロセッサのアーキテクチャ

DRAMからのメモリ・ロードは何百クロック・サイクルにも及ぶことがあるため、命令がメモリのフェッチ待ちの間に他の命令を処理することが望ましい。また、GPUには同じ操作を大量のデータに並列して適用することが期待される。このことから、GPUは1コアあたり数千ものスレッドを生成し制御できる。このようなGPUのアーキテクチャはSIMT (単一命令複数スレッド, Single-Instruction Multiple-Thread)と呼ばれる。コア内のスレッドはワープ(warp)というグループにまとめられた上でタスクを依頼される。

[!NOTE] GPUはSIMDって書いてある資料もあるけど？ 当初のGPUはSIMDだったが、グラフィックスから高度なシェーダー処理や汎用処理を志向にするにつれて、並行処理できるデータの量が可変ではないことがオーバーヘッドになった。そのため、ワープを最小単位として命令毎にワープの数を可変にできるSIMTとなった。

未分類

  1. Why called JK flip-flop? ↩

  2. コンピュータシステムの理論と実装 ↩