til
機械学習 (machine learning) (深層学習を除く)
ページの構成の際、次の情報源を参考にした。
- 機械学習 (東京大学工学教程)
- パターン認識と機械学習 上下
- ITエンジニアのための機械学習理論入門
- ゼロから作るDeep Learning
概要
機械学習の手法は、パラメトリックとノンパラメトリックに大別されます。
- パラメトリックモデルは、次の手順で推定します1
- パラメータを含むモデルを設定する
- パラメータを評価する基準を決める
- 最良の評価を与えるパラメータを決定する
- ノンパラメトリックは、パラメータを設定しません。十分なデータがあり、かつ事前知識が少ない場合に適しています。
パラメトリック手法において、パラメーターを評価する基準を求める関数をobjective function(目的関数)といいます。また、最良の評価を与えるパラメータを決めるためには最適化のアルゴリズムを決める必要があります。
| 手法 | パラメトリック | 目的関数 | 最適化アルゴリズム | タスク |
|---|---|---|---|---|
| 最小二乗法 | パラメトリック | 誤差関数 | 解析的に求まる | 回帰 |
| 最尤推定法 | パラメトリック | 尤度関数 | 解析的に求まる | 回帰 |
| 単純パーセプトロン | パラメトリック | 誤差関数 | 確率的勾配降下法 | 分類 |
| ロジスティック回帰 | パラメトリック | 尤度関数 | IRIS法 | 分類 |
| k平均法 | 二重歪み | クラスタリング | ||
| k近傍法 | 分類 | |||
| EMアルゴリズム | ||||
| SVM | ||||
| 決定木 |
機械学習のタスクと分類
機械学習の学習手法
モデルの評価にあたって、性能が過学習によるものではないことを示す必要がある。そこで、データセットを学習用とテスト用にランダムに分けることが考えられる。また、ハイパーパラメータの調整用に、さらに検証データを分けることもある。
MinMax法
WIP
機械学習のアルゴリズム
線形回帰モデル
最小二乗法
最小二乗法において、重みを解析的に導くための式展開は次の通り。誤差関数の$\frac{1}{2}$は微分した際の係数2を相殺するための定数。

なお、方程式を重みについて解くために、偏微分によって現れるデザイン行列のグラム行列が逆行列を持つことを示す必要がある。デザイン行列が 列数 ≦ 行数 のとき(つまり特徴数よりバッチサイズが大きいとき)、グラム行列は正定値であり、逆行列を持つ。
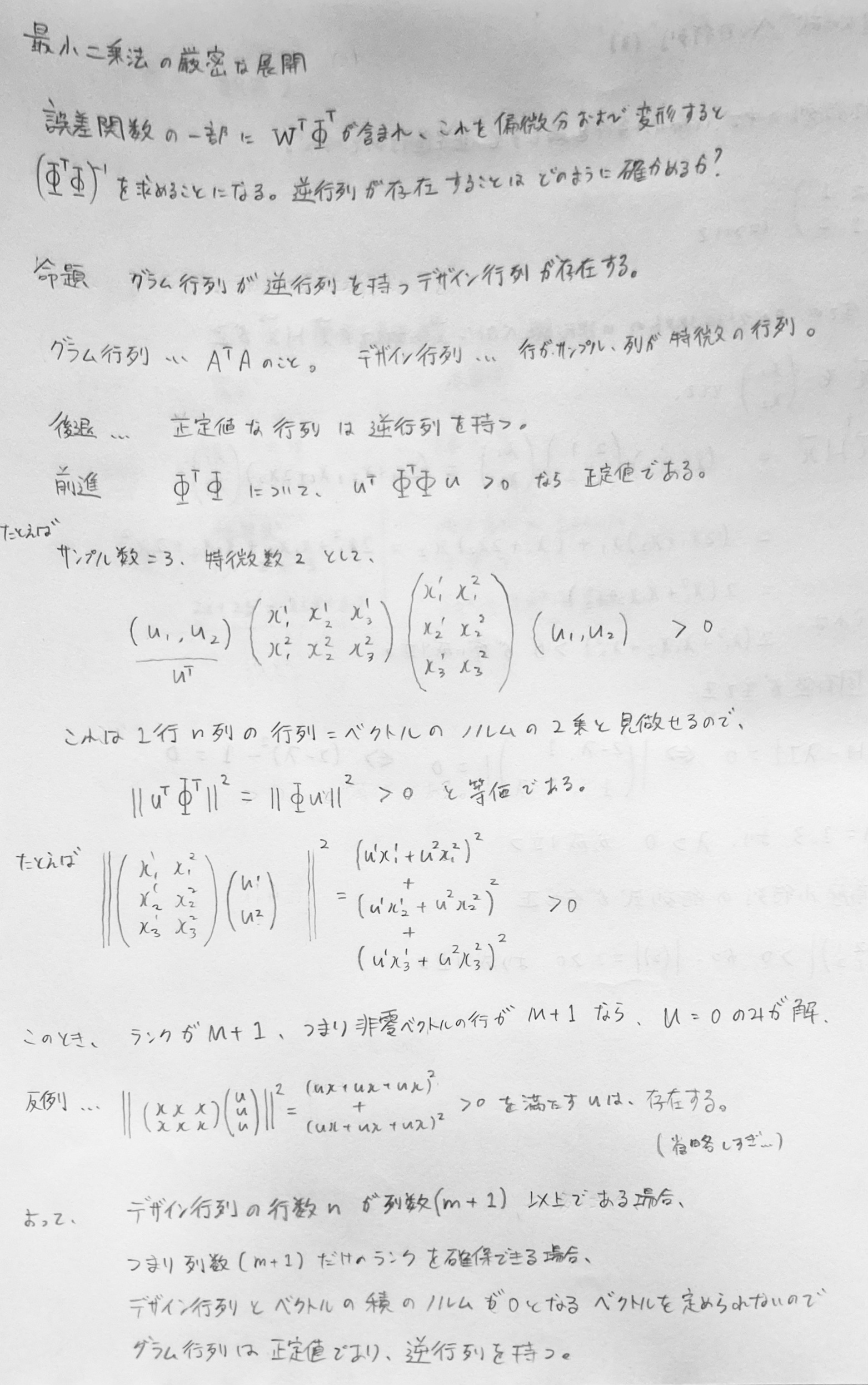
最尤推定
尤度関数は次の通り。なお、確率分布として正規分布を採用している。
| $P = \prod_{n=1}^{N} N(t_n | f(x_n), \sigma^2)$ |
線形識別モデル
単純パーセプトロン (perceptron)
パーセプトロンとは、説明変数から0か1を出力する二値分類モデルである。このモデルでは、バイアス項1を含む説明変数と重みを線形結合し、その結果にステップ関数(閾値関数)を適用する。ステップ関数は、線形結合の結果が閾値(通常0)以上なら1を、そうでなければ0を返す。ここでは、入力層と出力層が1層ずつの単層パーセプトロンを考える。
ステップ関数を使用しているため、出力の0と1の間の変化が不連続である。そのため、重みに関して偏微分して解析的に解くことができない。 また、ステップ関数を適用する前の値(線形結合の値)に対する目的変数は与えられていないため、線形結合前の値で解析的に解くこともできない(もし与えられていたら線形回帰になってしまう)。

解析的に解く代わりに、徐々に重みを正確にする方法がいくつか挙げられる。
パーセプトロン学習則では、誤分類されたデータに対して、説明変数に学習率をかけた値を直接重みから引く(または足す)。[^biopapyrus_2021] [^biopapyrus_2021]: パーセプトロン学習則
一方で、誤分類されたデータに対して、線形結合を重みに関して偏微分し、その勾配の方向に重みを更新することで、誤差を減らす方法がある。これを勾配降下法という。データをランダムに選んで更新を行う方法を特に確率的勾配降下法と呼ぶ。

ロジスティック回帰
ロジスティック回帰という名前だが分類のアルゴリズム。ロジスティック回帰は回帰か分類かも参照。
カーネル法
疎な解を持つカーネルマシン
SVM
分類・回帰アルゴリズムの1つ。データを分離する超平面を探す点はパーセプトロンと同じだが、超平面付近の点(サポートベクター)とのマージンを最大化することで汎化性能を引き上げている。また、データを高次元空間に写像することで、元の空間では線形分離できないデータを分離できるようになる。
グラフィカルモデル, 系列データ
ベイジアンネットワーク
条件付き確率の依存関係を有向非巡回グラフで表したものをベイジアンネットワークという。単純な分解では全てのノード間に辺が存在するため、逆にどのノード間に辺が無いかによってその確率が特徴づけられる。ベイジアンネットワークで見る変数の因果関係も参照。
マルコフ確率場
確率変数どうしがお互いに依存している関係を無向グラフで表したものをマルコフ確率場という。例えば、2x2ピクセルの画像の隣接するセルどうしは、同じ色である確率が高いため、マルコフ確率場で表せる。
カルマンフィルタ
ロボット制御などで、センサーの情報から実世界の乗法を推測することを考える。単純な例として、温度計が24度を示し、測定誤差が±1度であることを知っているとする。また、現在までに推定した温度が22度、その不確かさが±4度とする。ここで、新たな温度と不確かさを次の通り求める。[^geolab_kalman01] [^geolab_kalman01]: 第1回 カルマンフィルタとは
- 現在までの推定の不確かさと測定誤差の比を取る。このとき、現在までの推定の不確かさの割合をカルマンゲイン(K)とする。
- 新しい推定値 = K x 測定値 + (1-K) x 現在までに推定した温度 とする。
- 新しい不確かさ = (1-K) x 現在までの推定の不確かさ とする。
つまり、測定値と現在までの推定値の、不確かさによる重み付き平均で新しい推定値を表し、次に測定誤差が小さいほど新たな不確かさが小さくなるように重み付けをしている。
混合モデルとEM
k近傍法 (k-nearest neighbor algorithm)
分類アルゴリズムの1つ。例えば、天気を予測する問題を考える。気温・湿度・風速が与えられており、過去のデータ(教師データ)が利用できるとする。このとき、入力データを気温・湿度・風速の3軸からなる3次元空間にプロットし、最も近いk個のデータのラベルで多数決を取って、そのラベルを入力データのラベルの予測とする。このアルゴリズムをk近傍法といい、特にk=1の時に最近謗法という。データセット上のすべてのテントの距離を計算する必要があるため、データのサイズが大きい時にそのまま使うと時間がかかる。
また、過去のデータをそのまま用いるのではなく、ラベル毎にデータの重心を求め、入力データから最も近い重心のラベルを予測に用いるアルゴリズムをNCC (Nearest Centroid Classifier, あえて訳せば最近傍重心法)という。
k平均法 (k-nearest means algorithm)
クラスタリングの手法。NCCを教師なし学習で行う。といっても、教師データがないためにラベルがないから、適切な重心がどこだか分からない。そこで、初めに適当な位置に重心をばらまく。次に、重心毎に入力データを分類し、分類されたデータの重心を新たな重心とすることを繰り返す。このアルゴリズムをk平均法という。
EMアルゴリズム
WIP
近似推論法
サンプリング法
マルコフ連鎖モンテカルロ
円周率を近似する有名な方法にモンテカルロ法がある。円とそれに接する正方形めがけてランダムに粒を撒き、円に入った数と正方形に入った数の比から円周率を求める方法である。
マルコフ連鎖で表される状態遷移を考える。例えば、前日の天気に応じて今日の天気が決まるとする。前日の天気が分からなくても、それぞれの天気の変わりやすさ(例えば、晴れの翌日は70%晴れ、とか)が分かっていれば、分からないなりに一番当たりそうな天気を言うことができそうだ。確率過程の言葉で言えば、単純な天気のような場合は、連立方程式を解いて定常状態を求めることができる。しかし、例えば分子の動きのシミュレーションのように、状態(この場合はそれぞれの分子)が多すぎて解析的に定常状態を求められなかったらどうするか。ここでモンテカルロ法を用いる。つまり、ランダムな初期状態から求めたい時点での状態を計算することを無数に繰り返し、そこから確率分布を見出す方法である。
連続潜在変数
主成分分析
次元の多いデータを説明するにあたって、主な成分とそれを補う成分で説明できると全体像が分かりやすい。例えば、中学校のある学年のテストの成績のばらつきを説明する時に、「国語は〇〇で得意不得意が分かれて、数学は✗✗で〜」と全て説明するより、「総合成績で見ると3グループに分けられます。平均的なグループは、文系科目と理系科目で次のように分かれます…」のような説明の方が、頭の中で順を追って思い出しやすい。
次元削減の手法の中でも、データの特徴を最もよく表す次元から順に見出す方法として主成分分析(PCA, Principal Component Analysis)がある。[^intage_401]手順としては、射影した時にすべての次元の特徴の分散が最大になるような線を初めに引き、次にその線と直行する線の中で、同様に射影すると分散が最大になるような線を選ぶ。このようにして、データを説明できると判断できるところまで線、つまり成分を選ぶ。なお、これは相関行列の固有値分解と等価であるそうだ。 [^intage_401]: 主成分分析とは
各種成分は元の特徴量の線形結合なので、PCAは線形な手法と言える。
PCAはニューラルネットワークに対しても適用することができる。例えば、隠れ層の値を視覚化し、似たデータが近くにあるかを分析することは、モデルが適切に学習できてない場合の原因を探ることに役立つ。
多次元尺度法 (MDS)
アンケートなどの5段階評価のような手法を尺度法という。ちなみに、同意の度合いを測るものをリッカート尺度法、真逆の形容詞のどちらに近いかを測るものを評定尺度法という。
データを低次元に射影するにあたって、データ間の距離(ユークリッド距離が一般的だが、それ以外でも良い)を保つように射影する方法を多次元尺度法という。
t-SNE
PCAのような線形な手法では、複雑な非線形構造を持つデータの局所的な関係性を保持することが困難であった。t-SNEでは、高次元空間におけるデータどうしの類似度を、データ$x_1$を選んだ後にデータ$x_2$を選ぶ条件付き確率として定義している。その結果、t-SNEでは局所的な関係性を可視化できるようになった。
UMAP
モデルの結合
ブースティング
決定木
分類・回帰アルゴリズムの1つ。フローチャートによる分類を考える。例えば、お客さんにパソコンをオススメする。パソコン初心者で、かつ授業でも使うなら、Windowsを搭載したノートPCが良いだろう。このように、入力データのパラメータに応じて根から木をたどり、葉にたどり着いたら提案を行うモデルを決定木という。タスクによって分類木、回帰木ともいう。
決定木は性能が低いが計算コストが安い。そこで、複数の決定木を用意し、それらの重み付き多数決で予測を行うこととする。このような手法をアンサンブル学習といい、特に決定木で行う場合をランダムフォレストという。
機械学習の評価方法
予測の精度を測る指標は次の通り。
- 正解率 (Accuracy)
- 全ての予測に対する、正しい予測の割合
- 適合率 (Precision)
- $TP/(TP+FP)$
- 件数を減らしてでも偽陽性を防ぎたい場合に良い指標になる。ホワイトリスト向き
- 再現率 (Recall)
- $TP/(TP+FN)$
- 件数を増やしてでも偽陰性を防ぎたい場合に良い指標となる。ブラックリスト向き
- 例: セキュリティのアラート
- F値 (F-measure)
- 適合率と再現率の調和平均
前述の指標を踏まえて、機械学習の評価に用いられる指標は次の通り。
- ROC曲線 (Receiver Operating Characteristic曲線)
- 縦軸に真陽性率(=再現率)、横軸に偽陽性率を置いたグラフ
- 再現率を上げようと何でも陽性で判定すると、同時に偽陰性も増える、というトレードオフを表している
- PR曲線 (Precision-Recall Curve)
- 縦軸に適合率、横軸に再現率を置いたグラフ