til

確率論 (probability theory)

ページの構成の際、次の情報源を参考にした。

期待値, 分散, 標準偏差 (expected value, variance, and standard deviation)

[!NOTE] 標準偏差の計算では、分散の分母$N$まで含めて平方根を取る。にも関わらず、母数が過小評価されないのはなぜか？ 標準偏差は$N$の平方根を取るにも関わらず、母数が過小評価されない、つまりデータ数が増えるほど標準偏差が増えることはありません。 標準偏差の代わりに、分散の分子だけを平方根で括った指標で不都合があることを、次の通り証明します。 formula

演算の公式

期待値・分散の世界にも、微分積分の世界における合成関数のような概念があり、変数変換と呼ぶ。

標本に対する確率

標本の全てのデータに対する同時確率は、標本を示す記号を使って書いて良い。例えば$X=(x_1, x_2,…x_n)$とするなら、次の等式が成り立つ。

$P(x_1, x_2,…,X_n) = P(X)$

多次元の確率変数

$P(X,Y)$のような、複数の変数がある確率分布を考える。選挙における年代別の投票先を例に取る。このとき、投票先が〇〇党の場合の年代の期待値を知りたいとする。これを条件付き期待値という。Xを年代、Yを投票先とすると、求める値は$E[X Y=〇〇党]$と表せる。
手元に個別の調査結果があるなら直接数えられるが、そうでなく集計結果しかない場合も同時確率$P(X,Y)$と周辺確率$P(Y)$から求められる。つまり、同時確率で重み付けしたXの値$\sum_x x P(X=x,Y=〇〇党)$を、〇〇党に投票したことを前提にして良いので、周辺確率$P(Y=〇〇党)$で割ることで求める。これは、ベイズの定理に基づいて事後確率$P(X Y)$を求め、それを重みとした平均を求めると考えても同じである。

中心極限定理

平均と分散は同じだが、確率分布の形状が異なる標本がいくつかある。これらの標本からそれぞれ確率変数を取り出し、その平均を取る。標本の数が無限に近づくとき、その平均の値は$N(\mu, \frac{\sigma^2}{n})$に従う。

例として、投資のポートフォリオを考える。個々の株価の動きは正規分布ではないかもしれないが、十分に分散投資したポートフォリオの値動きはおおよそ正規分布となる。

k次のモーメント・モーメント母関数, 積率母関数 (moments and moment generating functions)

確率分布の性質を知るためには、期待値や分散、歪度、尖度が役に立つ。これらを導出するためには、確率変数$X$の$k$乗の期待値が便利である。 これを$k$次のモーメントと呼ぶ。

また、それらを体系的に扱うためのツールとしてモーメント母関数がある。モーメント母関数をマクローリン展開するとモーメントが得られ、期待値や分散の算出に役立つ。（マクローリン展開ってグラフなどを書きづらい関数を近似して雑ながらも書こう、という気持ちで理解していたから、すでに完成している関数を部品取りのためにマクローリン展開するのってなんか背徳感あるな…）

確率分布

性質 離散型確率分布における定義 連続型確率分布における定義
確率関数1 確率質量関数 確率密度関数
分布関数2    

確率質量関数のグラフを描いた際、Y軸はその事象が発生する確率であり、1を超えることはない。一方、確率密度関数におけるY軸の値は1を超えることがある。連続型確率分布において特定の事象が発生する確率を求めることはできないので、ある区間に数値が収まる確率を求めることになる。したがって、確率密度関数においてY軸が1を超えていたら、「面積の合計は1になるはずだから、分散が小さいのかもしれないなぁ」位に思っておけば良い。

離散型確率分布 (discrete probability distribution)

ベルヌーイ試行, ベルヌーイ分布

成功か失敗かの事象を0か1で表した試行をベルヌーイ試行といい、その確率分布をベルヌーイ分布と呼ぶ。

二項分布, 二項定理 (binomial distribution, binomial theorem)

$(a+b)^3$のような2項の累乗を、次の式で表せることを二項定理という。

$(a+b)^n = \sum_{k=0}^n \binom{n}{k}a^{n-k}{b^k}$

（ここで$\binom{n}{k}$とは${}nC_k$を指す。計算方法は、「n通り、n-1通り、…から1つ選ぶをk回繰り返し、重複を避けるためk!通りで割る」なので、$\frac{\prod{i=0}^{k-1}(n-i)}{k!}$である）

それ自体は中学校の数学で習うのだが、この式はそのまま、「成功か失敗かのいずれかの結果になる事象をn回行い、k回成功する確率」を求めるために利用できる。

ベルヌーイ分布, 二項分布の期待値, 分散の導出は次の通り。

ベルヌーイ分布, 二項分布の期待値, 分散の導出

ポアソン分布 (Poisson distribution)

単位時間あたりにn回成功するベルヌーイ試行が、m回成功する確率分布をポアソン分布という。

ポアソン分布の導出

幾何分布 (geometric distribution)

ベルヌーイ試行が初めて成功するまでに何回かかるかの確率分布を幾何分布という。

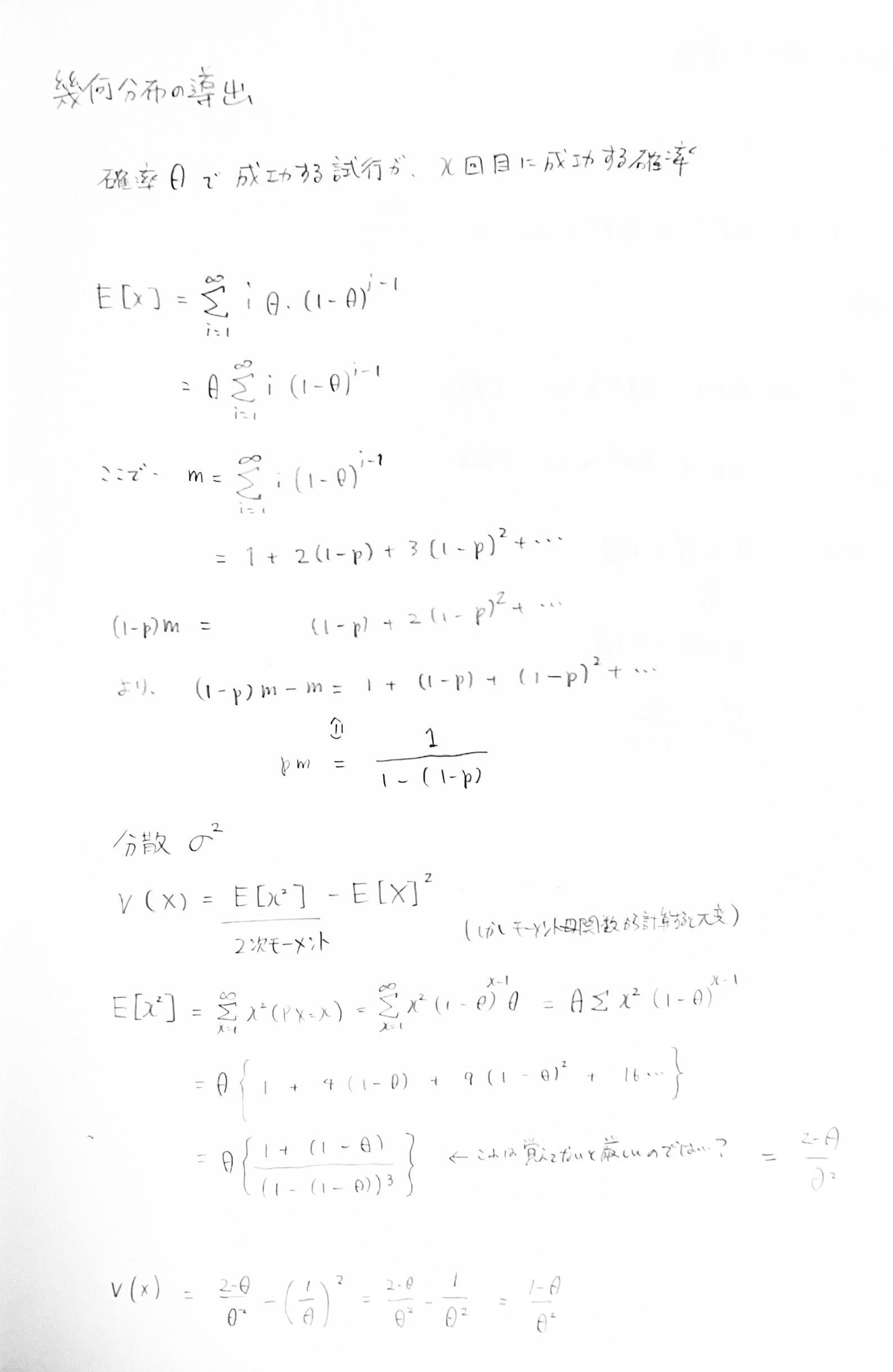
幾何分布の導出

負の二項分布 (negative binomial distribution)

ベルヌーイ試行がn回成功するまでの過程の確率の分布。失敗回数を指す場合と、合計の試行回数を指す場合とがある。

合計の試行回数を指す場合、それぞれの試行が独立なので、幾何分布の期待値と分散をn倍すると期待値と分散が求められる。

連続型確率分布 (continuous probability distribution)

統計 (statistics)

統計学の分類について、次の通り。[^ueniki_2022] [^ueniki_2022]: ベイズ統計学入門 〜頻度主義からベイズ主義へ〜

記述統計

測定の不確かさ (uncertainty)

長さや重さなどの精密な測定を依頼されたとする。測定結果は普通、$100g \plusmn 5g$のように区間で示す。一方で、確率的に大きさが変わるノイズを真の値に加えたものを測定結果とする考え方もある。後者のノイズを標準偏差で表したとき、それを合成不確かさといい、それを区間に変換した値を拡張不確かさという。

合成不確かさは、要因（温度, 湿度, 測定者, etc…）毎の不確かさを合成して求める。要因毎の不確かさを標準不確かさという。ここでは標準不確かさを、実際の測定から求める方法について述べる。真の値に対する測定値のばらつきは、統計学でいえば母集団に対する標本のばらつきと言い換えることができ、つまり標準偏差である。ところが、測定結果というのは一度測って報告するわけではなく、その平均などを報告する。だから、個別の測定値よりも標準偏差が小さくなるはずである。そこで、次の通り標準偏差を繰り返し回数の平方根で割ったものを標準不確かさという。

\[\begin{align} S(\bar{X}) = \frac{S(X)}{\sqrt{n}} \end{align}\]

測定の不確かさについて（初級編）も参照。

推測統計 (頻度主義統計学)

推測統計はその目的によって推定と検定に分けられる。また、特定のデータの分布を仮定するかどうかでも分けられる。次の表にまとめた。

分類 パラメトリック ノンパラメトリック
推定 点推定, 区間推定, 回帰分析 ノンパラメトリック回帰, カーネル密度推定, ブートストラップ法
検定 t検定, 分散分析(ANOVA) Mann-Whitney U検定, etc…

サンプルから母集団の統計量や変数同士の関係を予測することを推定という。推定された母集団の統計量を推定量という。

推定量の性質として、一致性と不偏性がある。サンプル数を増やすほど推定量が統計量に近づくことを一致性、サンプル数が多いときも少ないときも外れ具合が変わらないことを不編性という。

推定に対して、仮説が正しいかどうかを確かめることを検定という。

回帰分析

入力データの説明変数から目的変数を予測することを回帰分析という。説明変数が複数ある場合は（重積分のように）重回帰分析と呼ばれる。

t検定, 分散分析 (ANOVA), 共分散分析 (ANOCVA)

複数のデータ群の違いを測るにはどうしたら良いか。例えば、収穫された野菜の量を、農薬のありなしのデータ群で比較したいとする。データ群の平均の差を測ることが考えられるが、元々農薬があってもなくても変動する幅の範囲内かもしれない。そこで、データ群どうしの差と、データ群内の分散を比較することが考えられる。ここで、2つのデータ郡を比較することをt検定、複数のデータ群を比較することを分散分析という。

サロゲートデータ法

時系列データにパターンを見出したとき、それが偶然かどうかを決める根拠がほしい。ここで、偶然とした場合に差し支えないデータ（サロゲートデータ）を多数生成する。元のデータとサロゲートデータの統計量を比較し、元のデータがどれだけ稀だったかの確率を計算する。それが、事前に定めた水準より低ければ、偶然ではないとする。グラフフーリエ変換を用いたグラフ上のパターンに関する数理的解析も参照。

[!TIP] きょうは真夏日である。顔を洗おうとして水道の蛇口を捻ったら、はじめ水が冷たく、すぐにお湯になり、最後にまた冷たくなったように感じた。そこで、少し時間を置いてから、今度は1秒毎に水温を測った。

[27, 32, 31, 33, 32, 30, 28, 27]

この水温の変動が偶然なのかを確かめたい。この時系列データに時間的構造があるかを、サロゲートデータ法を用いて検定する。ただし、条件は次の通り。

  1. 帰無仮説は「データに時間的な構造がない」とする。
  2. 統計量として、隣接する温度の差の絶対値の合計を用いる。
  3. 有意水準を α = 0.05 とする。
  4. サロゲートデータを100個生成する。
解答 [surrogate_data_method.py](./_src/surrogate_data_method.py)を参照。

ベイズ統計学 (Bayesian statistics)

ベイズの定理 (bayes’ theorem)

ベイズの定理における用語は次の通り。

ベイズの定理

また、ベイズの定理を面積と計算グラフで表すも参照。

[!NOTE] 仮説を選ぶ際、事後分布を使う必要はある？同時確率で十分では？ 確かに、事後分布は同時確率の比を百分率で表したに過ぎないから、同時確率を使って仮説を選んでもいい。 ただし、同時確率はデータの珍しさに影響されてしまう。珍しいデータの時も、そうでない時も、一貫した意思決定をするためには、事後分布に基準を設けるのがよいだろう。

情報理論 (information theory)

この章を構成する際、次の情報源を参考にした。

情報量 (entropy)

ある事象の起こりにくさの尺度を情報量という。例えば、都内で雪が降ったらニュースになるが、晴れであることは特にニュースにならない。

ある情報源に対して、そのような情報量の期待値を平均情報量（エントロピー）という。それに対して、個別の事象の情報量は自己情報量（自己エントロピー）と言われる。平均情報量は期待値なので事象の起きる確率と情報量の積和である。その中で特定の事象の起きやすさを$1/N$にすると、情報量は対数なので$-log_2(N)$となる。つまり、起きる事象の種類が同じ場合、全ての事象の確率が均等（各1/N）な情報源の方が、確率に偏りがある情報源よりも平均情報量（エントロピー）が大きくなる。情報理論の基本原理として均等な均等な確率分布が最大のエントロピーを持つことが、ここから言える。

さて、機械学習でどの特徴変数と目的変数が最も関連しているかを知りたいとする。相関係数を使いたいところだが、相関係数は比例関係を扱うため、例えば周期的な関係では適切に関連性を捉えられない。そこで、（特徴変数と目的変数を適切に離散化してから）全ての可能な組み合わせの同時確率を測る。これによって算出した値を相互情報量という。例えば、特徴変数を睡眠時間、通勤時間、労働時間とし、目的変数をその日のストレスとする。睡眠時間とストレスが完全に結びついている場合、相互情報量は最大となり、いずれかの情報源の平均情報量となる（どちらを取っても等しい値のはず）。これは言い換えれば、睡眠時間とストレスのどちらかが分かればもう片方が分かるような状態を指す。逆に、全く結びつきがない場合、相互情報量は0となる。

対数の底が2の場合、情報量はビット(bit)で表す。また、底がeの場合はナット(nat)、10の場合はディット(dit)と呼ばれる。ナットは”natural unit of information”の略。

情報量の概念は、モデルの良さを測るためにも使える。分類モデルを考えると、予測されたラベルは数値ではないから、そのままでは誤差を測ることができない。ただし、教師あり学習の場合は正解ラベルとの一致・不一致を数えることはできる。また、クラスタリングなどの教師なし学習の場合は、特徴空間における座標を使って類似度や距離を測ることができる。学習において、正しい分類だが低い確信度を引き上げるよりも、誤った分類の高い確信度を引き下げるほうが重要である。そのフィードバックに距離を用いてもよいが、医療診断のように予測の確実性が重要な場合は、確実性を直接最適化したい。そうした場合、予測の確実性を確率分布として直接比較する手法として交差エントロピーがある。交差エントロピーでは、平均情報量の積和にあたって、真の分布の確率と予測分布の情報量の積を和の対象とする。最小値は真の分布のエントロピー、最大値は無限大となる。

モデルの良さを記録するにあたって、交差エントロピーの値は真の分布に依存するため、複数の分布・モデルの組を比較する際に数値が意味をなさないという問題がある。そこで、交差エントロピーから真の分布の情報量を引いた値をカルバック・ライブラー情報量(相対エントロピー, KLD, Kullback-Leibler divergence)と呼び、相対的な比較と評価の道具として用いることができる。

しかし、離散分布であってもKLDを計算できるのはサンプルサイズが十分に大きい場合に限られるし、連続分布では真の分布が明らかでないとKLDの計算はできない。真の分布が不明でもモデルの良さを測る指標が赤池情報量規準(AIC, Akaike Information Criterion)である。$AIC=-2\cdot (最大対数尤度) + 2 \cdot (パラメータの数)$で計算される。尤度が同程度なら、過学習などを避けるためにパラメータ数が少ないほうがよい、という動機と思われる。[^karasawa_2020] [^karasawa_2020]: AIC（赤池情報量基準）を学ぶ

符号理論 (coding theory)

通信路

距離

文字数が同じ2つの単語、例えばcatとcarで、異なる文字数の数（この場合は1）をハミング距離という。単語と書いたが、もちろん文字列に拡張して考えてよい（意味のない文字列でも良いってこと）

ネットワーク上で0と1からなる情報を通信した際、ノイズによっていくつの0と1が誤ってしまったかを数えるために用いられた。

これを文字数が異なる文字列に拡張したのがレーベンシュタイン距離である。例えば、loveとmoneyのレーベンシュタイン距離は3である。

誤り訂正

情報を送る際、ビットの和が奇数か偶数かを予め相手に伝えておく。さらに情報の末尾に、ビットの和が奇数か偶数になるように1ビットを付与する。これを奇数/偶数パリティと呼ぶ。

パリティは情報の誤りを検知することができるが、訂正まではできないため、誤っていたら再送信するしかない。そこで訂正のために、パリティを賢く増やすことを考える。

パリティを賢く増やすとはどういうことかというと、情報の中に同じパリティの組合せに所属するビットが1つもないようにすることである。図で考えやすくするために、8ビットの情報を送ることを考える。8ビットの情報は、2マス×2マス×2マスのキューブとして捉えられる。この時、縦・横・高さの3軸でそれぞれパリティチェックを行う側・行わない側を設けると、全てのビットでパリティチェックの組合せが一意になる。ここで、全てのパリティチェックを避けた1ビットを除いた7ビットが、受信側で誤り訂正が可能な符号といえる。なお、余った1ビットは全体のパリティチェックに用いる。これをハミング符号化と呼ぶ。資料も参照。3

余談だけど、周期の異なるパリティを複数重ねることで誤り訂正に強くなる、って考え方は、独立な多数の因子の和として表される確率変数が正規分布に従う中心極限定理に似てるなと思った。

通信路の容量, シャノンの定理

確率過程

この章の学習にあたって次の情報源を参考にした。

確率過程モデル

イベントや時間など、条件によって値が変化する事象を、確率変数の変化と捉えた時、確率過程モデルという。

状態の変化が直前の状態のみに依存し、かつ状態が離散的なものをマルコフ連鎖 (Markov chain)といい、状態が連続的なものをマルコフ過程 (Markov process)ということが多い。[^yasuda_kakukatei] [^yasuda_kakukatei]: 確率過程

観測可能な状態が隠れた状態に依存しているモデルを隠れマルコフモデルという。例えば、遠距離に住んでいる友達と毎日通話して、その日に起きた出来事を聞く。聞いた内容（例えば、散歩や読書）から、友達の住んでいる場所の天気を推測する。これは隠れマルコフモデル的と言える。[^satomacoto_2008] [^satomacoto_2008]: 隠れマルコフモデルの例

離散時間確率過程

待ち行列とは

待ち行列モデル

ケンドールの記法によって、次の通り表される。

待ち行列の応用

  1. 確率関数という言葉が何を指すかは曖昧である。マセマに準じれば、単に確率関数と言った場合は確率質量関数を指す。 ↩

  2. 単に分布関数といえば、累積分布関数を指す。 ↩

  3. 符号化と通信の理論 ↩